3. Repair Process and Spare Architectures
3.1 Memory Repair Process

Memory test and repair process는 hybrid RA 접근법을 통해 일반적으로 진행된다.
테스트 중에 test pattern을 적용하면서 fault cell이 발견되면 해당 fault information은 나중에 수리를 위해 저장된다.
Test time과 repair time을 줄이기 위해 preprocessing/filter algorithm이 적용된다. 이는 early-abort condition을 충족하는 메모리를 irreparable memory로 분류해 필터링하고 불필요한 추가 절차를 피하며 프로세스를 종료한다.
Memory test가 끝난 후 RA algorithm은 faulty cells를 수리할 solution을 찾는다.
마지막으로, faulty memory는 faulty cells를 good spare cells로 교체함으로써 수리된다.
Static RA와 dynamic RA 접근법 모두 기본적인 test-and-repair procedure를 공유한다. 그러나 static RA는 faulty cells를 수집한 후 RA process를 실행하므로 preprocessing/filter algorithm을 적용할 수 없다. 반면 dynamic RA는 memory test와 RA process가 동시에 종료되기 때문에 preprocessing/filter algorithm이 필수적이지 않다.
Software-based RA와 hardware-based RA는 결과적으로 동일한 결과를 내지만 그 과정에서 차이가 있다. Software-based RA는 Automated Test Equipment(ATE)에서 수행되며, ATE testing 중에 test pattern이 메모리에 적용된다. Faulty cell이 발견되면 ATE가 fault information을 수신해 fault bitmap에 저장한다. Software-based 알고리즘은 속도가 느리므로 preprocessing/filter algorithm을 통해 RA execution time을 줄여야 한다. Memory test 후 ATE 내에서 software-based RA algorithm이 repair solution을 찾는다.

Built-In Self-Test(BIST)와 BIRA를 함께 사용하는 Built-In Self-Repair(BISR) 메모리의 경우 BIST가 memory cell들에 대한 test patterns를 생성하고 faulty cell들을 찾아낸다. 발견된 fault information은 BIRA로 전송되어 storage elements(registers와 content-addressable memories, CAMs)에 저장된다. 이 요소들은 incoming data를 기존 데이터와 clock cycle 내에서 비교한다. BIRA는 RA algorithm에 따라 fault information을 분석하며, BIST와 BIRA의 area overhead가 제한적이므로 preprocessing/filter algorithm으로 필터링된 fault information은 무시된다. 이 알고리즘은 software-based RA와 유사하게 analysis time을 줄인다. Memory test가 끝나면 칩에 내장된 BIRA hardware가 repair solution을 찾는다.
3.2 Spare Architectures

Spare architectures는 메모리 수리에 있어 중요한 역할을 한다. Figure 6(a)와 Figure 6(b)는 1D redundancy line architecture를 나타내며spare rows 또는 spare columns를 사용해 memory array를 수리한다. 1D 구조는 복잡한 RA algorithm 없이 간단한 repair solution을 제공한다. Faulty memory cell이 발견될 때마다 faulty row나 column이 extra rows나 columns에서 가져온 spare element로 교체된다. 이전에 spare line으로 수리된 주소에서 새로운 faulty cell이 발견되면 이미 수리된 것으로 간주된다. 하지만 orthogonal faulty lines를 수리할 수 없어 repair efficiency가 매우 낮다.
2D spare architecture는 spare rows와 spare columns를 모두 사용해 memory array를 수리한다. Figure 6(c)는 2D spare line architecture를 보여주며 4개의 faulty cells를 단 2개의 spares(1개의 spare row와 1개의 spare column)로 수리한다. 반면 1D architecture는 동일한 상황에서 3개의 spares가 필요하다. 이 때문에 2D architecture가 faulty memories 수리에 더 널리 사용된다. 그러나 spare lines의 수가 제한적이어서 faulty cells가 많을 경우 repair rate가 감소한다.
이를 개선하기 위해 configurable spares를 갖춘 새로운 2D architectures가 제안되었다고 한다. RAM의 word-lines와 bit-lines를 분할하며, 예를 들어 1개의 spare row를 2개의 spare blocks로 나누면 각 block이 2개의 orthogonal faulty cells를 수리할 수 있다. 이 구조는 bit-oriented와 word-oriented memory array를 구분하지 않고, spare words를 유연하게 할당해 traditional 2D spare architecture보다 repair efficiency가 높다. 1 word가 2비트를 차지한다고 가정할 때, (3, 6)의 faulty cell을 (4, 6)으로 재배치하면 1개의 spare row와 1개의 spare column으로는 수리할 수 없지만, 2개의 words와 1개의 spare column으로 추가 spares 없이 수리 가능하다. 하지만 복잡한 control overhead가 존재한다.
4.1 Heuristic RA Algorithms with Non-Optimal Repair Rate
Heuristic RA 알고리즘은 빠른 분석 속도를 제공하지만 optimal repair rate를 보장하지 않는 특징을 가지고 있다. Repair-Most(RM)와 FAST 알고리즘을 중심으로 heuristic RA의 작동 원리와 장단점을 살펴보자.
4.1.1 Repair-Most (RM) Algorithm
2D RA의 복잡성은 NP-complete로 알려져 있어 빠른 analysis speed를 얻기 어렵다. 이를 해결하기 위해 Repair-Most(RM) 알고리즘은 faulty lines 내 faulty cells 수를 기반으로 한 단순한 알고리즘을 사용한다.
RM은 hybrid RA 접근법을 채택하며 must-repair phase와 final repair phase의 두 단계로 나뉜다. Must-repair phase에서는 각 row의 row-fault counter 값을 spare columns 수와 비교한다. 모든 row를 분석한 후 faulty cells 수가 spare rows보다 많은 column에 동일한 과정을 적용한다. 이 분석은 must-repair 대상 row나 column이 spare elements를 사용하지 않거나 spares가 모두 소진될 때까지 반복된다.
Final repair phase에서는 Row-fault와 column-fault counters를 내림차순으로 정렬하고 가장 많은 faulty cells를 포함한 faulty line을 수리한다. 해당 line에 spare가 있으면 faulty cells를 제거하고 counters를 업데이트하며 faulty cells가 없어질 때까지 반복된다. 모든 spares를 사용한 후에도 faulty cells가 남아 있으면 RM 알고리즘은 faulty memory를 수리할 수 없다. RM은 단순함과 속도로 인해 유용하지만 repair rate가 낮은 단점이 있다.
4.1.2 FAST Algorithm
RM 알고리즘의 지나치게 단순한 메커니즘은 repair rate가 낮다는 문제를 낳는다. 이를 개선하기 위해 FAST 알고리즘은 fault grouping 개념을 도입해 상대적으로 높은 repair rate와 빠른 analysis speed를 달성한다.
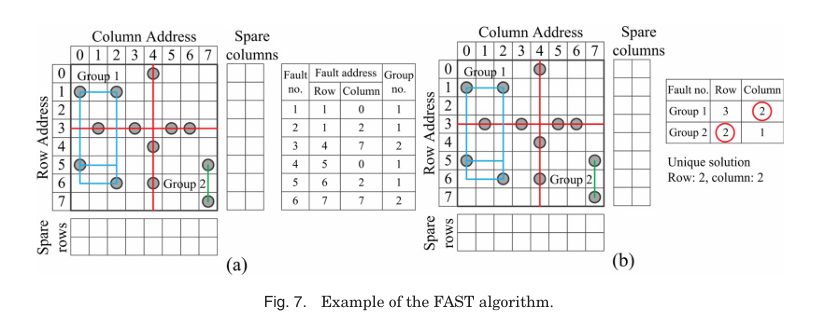
FAST는 hybrid RA 접근법을 사용하며 individual fault group들을 조직화한다. ATE memory test 중에 fault bitmap과 fault group이 동시에 형성된다. Fault group은 fault location과의 관계에 따라 single-fault group과 multiple-fault group으로 나뉜다. Multiple-fault group의 faulty cell들은 다른 faulty cell들과 주소를 공유한다. 새로운 faulty cell이 기존 fault group의 row나 column 주소와 같으면 해당 group에 합류해 multiple-fault group의 일원이 된다. 이 과정이 Figure. 7의 표에 나타나있따다.
FAST는 must-repair analysis, early termination condition, single faulty cell filter라는 세 가지 preprocessing algorithm을 사용한다. Group 수가 spare row와 column들의 합을 초과하면 메모리는 수리 불가능으로 판단된다. 이후 FAST 알고리즘은 모든 multiple-fault groups의 faulty row와 column 주소 수를 검사한다. Single-fault group은 single-fault만 포함하므로 검사 대상에서 제외된다. Single-fault는 FAST 알고리즘 적용 후 spare element로 수리 가능하다. Row와 column 주소 수를 available spares와 비교한 뒤, single-fault groups 수를 남은 spares와 비교해 solution을 도출한다. Figure 7(a)는 must-repair 분석 후 faulty memory 상태를 보여준다. Row 3과 column 4가 수리된 후 6개의 faulty cell과 2개의 fault group이 남는다.
Figure 7(b)는 multiple-fault groups의 주소 수를 나타내며, Group 1은 3개의 spare rows 또는 2개의 spare columns를, Group 2는 2개의 spare rows 또는 1개의 spare column을 필요로 한다. Solution candidates는 (R3, R2), (R3, C1), (C2, R2), (C2, C1)이며, (C2, R2)가 최종 repair solution으로 선택된다.(각 spare row와 column의 개수가 정해져있으므로 unique solution이 된다.)
4.2 RA Algorithms with Optimal Repair Rate
Optimal repair rate를 달성하기 위해서는 exhaustive search 알고리즘이 필수적이다. Exhaustive search는 모든 가능한 경우를 철저히 탐색하기 때문에 reparable memories에서 반드시 repair solution을 찾아낸다. 이 과정에서 faulty cell은 spare row 또는 spare column 중 하나로 수리된다. Binary search tree는 각 노드에서 두 가지 선택지—하나는 spare row로 가는 가지, 다른 하나는 spare column으로 가는 가지—를 제공하므로 exhaustive search에 매우 적합하다. ATE processor는 faulty cell이 발견될 때마다 binary search tree를 확장하며 분석이 끝나면 메모리가 수리 가능한지 여부를 결정한다.
4.2.1 Fault-Driven Algorithm
Fault-driven 알고리즘은 exhaustive binary search tree를 활용해 repair solution을 찾아내며 항상 optimal repair rate를 보장한다. 접근법은 두 단계로 나뉜다
첫 번째는 must-repair analysis, 두 번째는 sparse-repair(final-repair) analysis다. Must-repair analysis는 반드시 수리해야 할 faulty lines를 식별하며 sparse-repair analysis는 남은 faulty cells를 fault-driven 방식으로 처리한다.
첫 단계에서 생성된 root record는 두 번째 단계에서 solution record로 유지되며 모든 repair solution records는 이 root record를 기반으로 확장되고 업데이트된다. Faulty cell이 감지되면 solution records는 해당 cell의 row와 column 주소를 포함하도록 확장된다. 하나의 solution record는 두 개의 새로운 record로 분기되는데 하나는 row 주소로, 다른 하나는 column 주소로 확장된다. 만약 solution record에 available spare가 없다면, 그 record는 repair solution에서 제외된다. 따라서 각 solution record는 그 시점까지 감지된 faulty cells에 대한 유효한 repair solution으로 남는다.
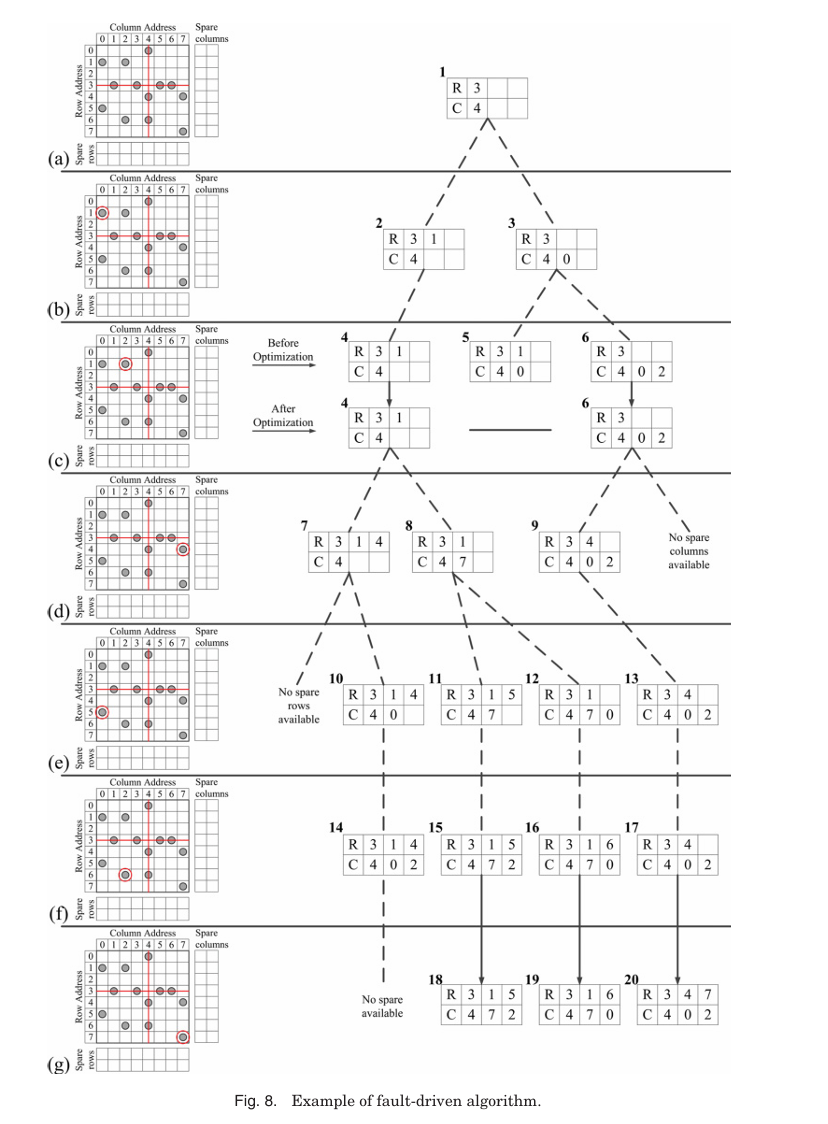
Figure 8을 통해 자세히 살펴보자. 메모리는 SR=3, SC=3으로 설정되어 있어 3개의 spare rows와 3개의 spare columns를 가진다. Faulty memory에는 총 13개의 faulty cells가 존재한다.
Must-repair analysis에서 row address 3은 4개의 faulty cells를 포함하고 있어 spare columns 수(3)보다 많다. 따라서 row address 3은 must-repair line으로 지정되고 1개의 spare row가 할당된다.
이어서 column address 4는 3개의 faulty cells를 포함하고 있으며, 이는 남은 spare rows 수(2)보다 많다. 그래서 column address 4도 must-repair line으로 지정되고 1개의 spare column이 할당된다.
이 과정을 통해 must-repair analysis는 1개의 faulty row와 1개의 faulty column을 수리하며 Figure 8(a)는 이 상태를 보여준다. 여기서 남은 자원은 2개의 spare rows와 2개의 spare columns이며, solution record 1이 초기 상태로 설정된다.
다음으로 faulty cell (1, 0)이 감지되면 cell의 row와 column 주소를 solution record 1과 비교한다. Solution record 1에는 아직 아무 주소도 없으므로, row address 1과 column address 0이 각각 solution records 2와 3에 추가된다. Figure 8(b)는 이 과정을 시각화한다. 이어서 faulty cell (1, 2)가 감지되면 모든 기존 solution records와 비교된다. Solution record 2는 이미 row address 1을 포함하고 있으므로 (1, 2)의 row address 1과 매칭되어 solution record 4로 유지된다.
반면 solution record 3에는 (1, 2)의 row나 column 주소가 없으므로, row address 1과 column address 2가 각각 solution records 5와 6에 새로 추가된다. Figure 8(c)가 이 상태를 보여준다.
Fault addresses는 감지된 faulty cells 순서대로 solution records에 저장된다. 이 과정에서 invalid solution records는 optimization을 통해 제거된다. solution record 5는 (R1, C0)을 포함하고 있어 faulty cell (1, 0)을 spare row와 spare column 모두로 수리하게 된다. 이는 중복 수리이므로 비효율적이며 Figure 8(c)에서 optimization 단계 후 solution record 5가 제거된다. 만약 spares가 모두 소진되면 더 이상 faulty cell 주소를 저장할 공간이 없어진다. 최종적으로 3개의 valid solution records(solution records 18, 19, 20)를 도출한다.
4.2.2 Branch-and-Bound Algorithm
실제 메모리 설계에서 spare row와 spare column의 embedding cost는 다르다. 이 알고리즘은 exhaustive binary search tree를 기반으로 spare cost-function을 활용해 optimal repair rate와 cost-effective repair solutions를 동시에 달성한다. Hybrid RA 접근법을 사용하며 첫 번째 단계는 must-repair analysis, 두 번째 단계는 branch-and-bound final analysis다.
각 tree 노드에는 cost function F가 할당되며 spares의 weighted values로 계산된다. spare rows에 가중치 8, spare columns에 가중치 15가 제안되었다.
여기서 R은 allocated spare rows의 수, C는 allocated spare columns의 수를 의미한다. 이 식은 spare column이 spare row보다 비용이 높다는 가정을 반영한다.
Branch-and-Bound는 항상 lowest cost를 가진 solution node를 선택해 확장하며 불필요한 가지를 pruning해 계산 효율성을 높인다. Must-repair lines는 root node(node 1)에 저장되며, faulty cell이 감지될 때마다 lowest cost node가 업데이트되어 해당 cell을 커버하고 비용을 누적한다.
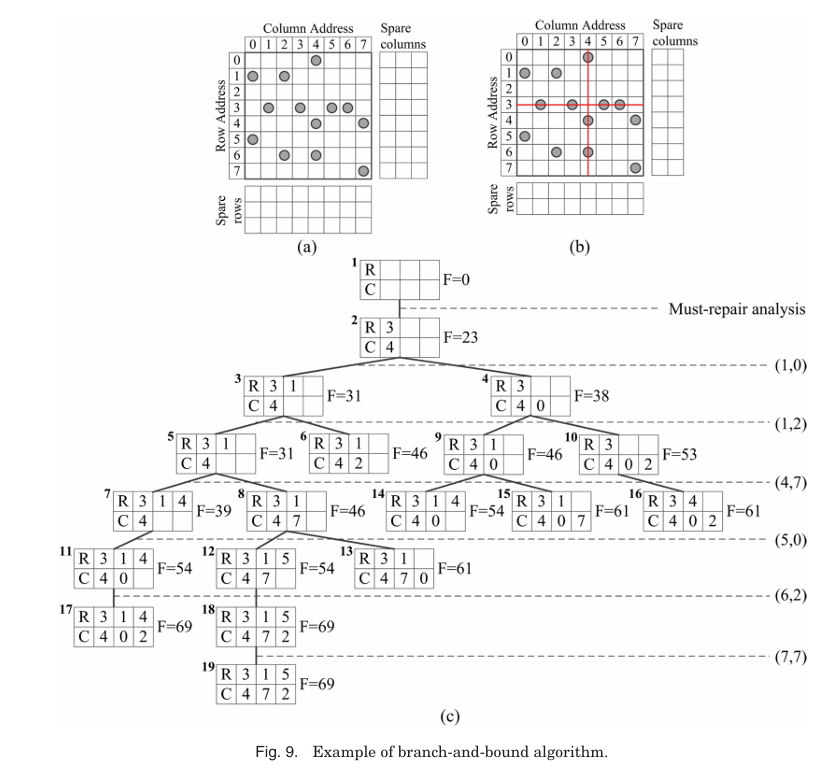
Figure 9는 이 알고리즘의 동작을 예시로 보여준다. Figure 9(a)는 SR=3, SC=3인 초기 메모리 상태를 나타낸다. 이전과 같이 Must-repair analysis에서 row address 3과 column address 4가 must-repair lines로 지정된다.
Node 2는 row address 3과 column address 4를 포함하며, F = 8 × 1 + 15 × 1 = 23이다. Faulty cell (1, 0)이 감지되면 node 2와 비교되고, 매칭되는 주소가 없으므로 node 3(row address 1 추가, F = 8 × 2 + 15 × 1 = 31)과 node 4(column address 0 추가, F = 8 × 1 + 15 × 2 = 38)가 생성된다.
다음 faulty cell (1, 2)은 lowest cost인 node 3(F=31)과 비교된다. Row address 1이 이미 포함되어 있으므로 node 5는 node 3의 상태를 유지하며 F=31이다. Node 6은 column address 2를 추가해 F = 8 × 2 + 15 × 2 = 46이 된다. Faulty cell (4, 7)은 다시 lowest cost node인 node 5에 추가되며, node 7과 node 8이 생성된다. 이 과정에서 node 4(F=38)가 가장 낮은 비용을 가지면 (1, 2)로 확장되어 node 9(F=46)와 node 10(F=53)이 생성된다. Node 7이 lowest cost가 되지만 spare row가 없으면 node 11이 생성된다. 이와 같은 방식으로 faulty cells [(5, 0), (6, 2), (7, 7)]이 처리되며, node 19가 최종 repair solution으로 모든 faulty cells를 lowest cost로 제거한다.
4.2.3 PAGEB Algorithm
Binary search tree 기반 알고리즘은 analysis speed가 느리다는 단점이 있다. PAGEB 알고리즘은 이를 해결하기 위해 RA 문제를 Boolean functions로 변환하고 binary decision diagram(BDD)을 사용한다.Hybrid RA 접근법을 사용하며, 첫 단계는 preprocessing/filter algorithms, 두 번째 단계는 Boolean transformation이다.
세 가지 Boolean functions—defect function(DF), constraint function(CF), repair function(RF)—가 핵심이다. Row와 column 제약은 직교하므로 CFr과 CFc로 나뉘며, CF는 CFr과 CFc의 곱이다. Replacement function(PF)은 제약을 직관적으로 표현하며, 다음과 같이 정의된다:
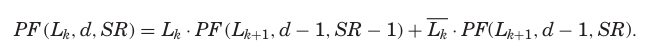
여기서 Lk는 k번째 faulty line(1이면 수리, 0이면 수리 안 함), d는 faulty line 수, SR은 spare row 수다. 이 식은 재귀적으로 동작하며 faulty line이 수리되면 spare가 1 줄고(Lk=1), 수리되지 않으면 spare가 유지(Lk=0)된다. PF의 속성은 spares가 faulty lines보다 많거나 같으면 true, spares가 없으면 false다.
Figure 10은 SR=1, SC=1인 메모리와 Boolean functions를 보여준다. 변수의 selecting order는 R1 < C1 < C3 < R3로 설정된다.
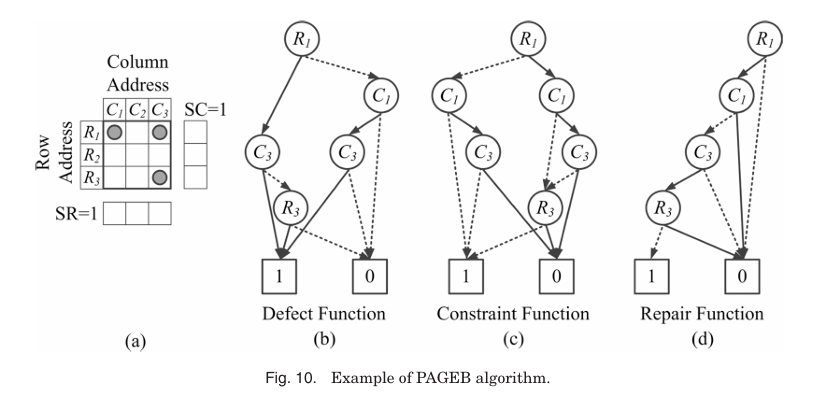
DF (Defect Function)
DF는 모든 faulty cell의 위치를 encoding한다 -> faulty cell (1,1), (1,3), (3,3)이 각각 R1 또는 C1, R1 또는 C3, R3 또는 C3으로 수리되어야 함을 나타낸다. (R1 + C1)은 (1,1)이 row 1이나 column 1로 커버될 수 있음을 의미한다. Figure 10(b)는 DF의 BDD를 보여준다.
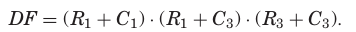
CF (Constraint Function)
CF는 reparable faulty lines의 모든 조합을 정의한다. CFr은 PF를 통해 계산된다:여기서 PF(L1, 1, 0)은 SR=0일 때 L1=0이어야 하므로 L1이고, PF(L1, 1, 1)은 SR=1일 때 항상 true다. CFc도 유사하게 계산되며, 최종 CF는 Figure 10(c)는 CF의 BDD를 나타낸다.
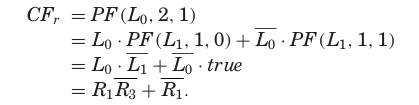
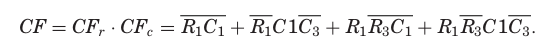
RF (Repair Function)
RF는 DF와 CF의 곱으로 reparability를 결정한다. Figure 10(d)는 RF의 BDD를 보여주며, 최종 repair solution은 (R1, C3)이다.
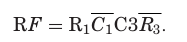
'DFT(Design for Testability)' 카테고리의 다른 글
| Test vector compression (0) | 2025.04.05 |
|---|---|
| [논문리뷰] A Survey of Repair Analysis Algorithms for Memories(3) (0) | 2025.04.01 |
| [논문 리뷰] A Survey of Repair Analysis Algorithms for Memories(1) (0) | 2025.03.28 |
| [논문 리뷰] An Overview of Processing-in-Memory Circuits for Artificial Intelligence and Machine Learning(DRAM PIM) (0) | 2025.03.24 |
| DFT(Design for Testability) (0) | 2025.03.20 |