2. Background
2.1. Performance Criteria
RA와 BIRA 알고리즘의 성능을 평가하는 기준은 analysis speed, repair rate, area overhead이다.
- Repair rate는 수리된 메모리 수를 테스트된 전체 메모리 수로 나눈 값으로 정의
- Repair rate = number of repaired memories / number of total tested memories
- Normalized repair rate는 수리된 메모리 수를 reparable 메모리 수로 나눈 값
- Normalized repair rate = number of repaired memories / number of reparable memories
Repair rate는 memory yield와 직결되며, RA와 BIRA는 이를 높여 yield를 극대화한다.(결함이난걸 repair해서 사용가능하게함) Normalized repair rate는 reparable 메모리에 초점을 맞춰 성능을 더 직관적으로 평가한다. Optimal repair rate에서는 normalized repair rate가 100%가 된다.
ATE(Automatic Test Equipment, 메모리 장치나 칩을 테스트하고 결함을 분석하기 위해 사용되는 외부 시스템)는 area overhead가 덜 중요하지만, BIRA는 hardware logic 때문에 area overhead가 큰 영향을 미친다. High-density 메모리는 faulty cell 확률과 spare 수(결함(faulty cell)을 수리하기 위해 미리 준비된 추가적인 셀(cell), 행(row), 열(column))가 많아 RA 시간이 길고 area overhead가 커진다. Faster RA speed와 낮은 area overhead는 test 비용을 줄이지만, speed, repair rate, area overhead 간 tradeoff가 존재한다. Optimal repair rate를 위해 exhaustive search algorithm이 필요하지만, 이는 시간이 오래 걸리고 큰 analyzer가 요구된다.
2.2. Preprocessing/Filter Algorithms
2D spare architecture의 redundancy allocation은 NP-complete 문제이다. RA 시간을 줄이기 위해 polynomial time complexity를 가진 preprocessing 및 filter algorithm이 사용된다.
Must-repair Algorithm
Must-repair algorithm은 메모리에서 필수적으로 수리해야 하는 faulty line(row 또는 column)을 식별하고 이를 spare row나 spare column으로 교체하는 알고리즘이다. 작동 방식은 장치의 각 row와 column마다 row error counter와 column error counter를 생성해 faulty cell 수를 계산하고, 이를 사용 가능한 spare row와 spare column의 수와 비교하는 것이다
한 row에 5개의 faulty cell이 있고 spare column이 4개라면 spare column만으로는 모두 수리할 수 없으므로 spare row를 사용해야 하며, 마찬가지로 한 column에 4개의 faulty cell이 있고 spare row가 3개라면 spare column으로 교체해야 한다. must-repair 대상인 faulty row를 모든 spare column으로 수리하려 하면 적어도 하나의 faulty cell이 남을 수 있고, 이 경우 reparable 메모리임에도 불구하고 solution을 찾지 못하는 한계가 있다.
Early-abort Algorithm
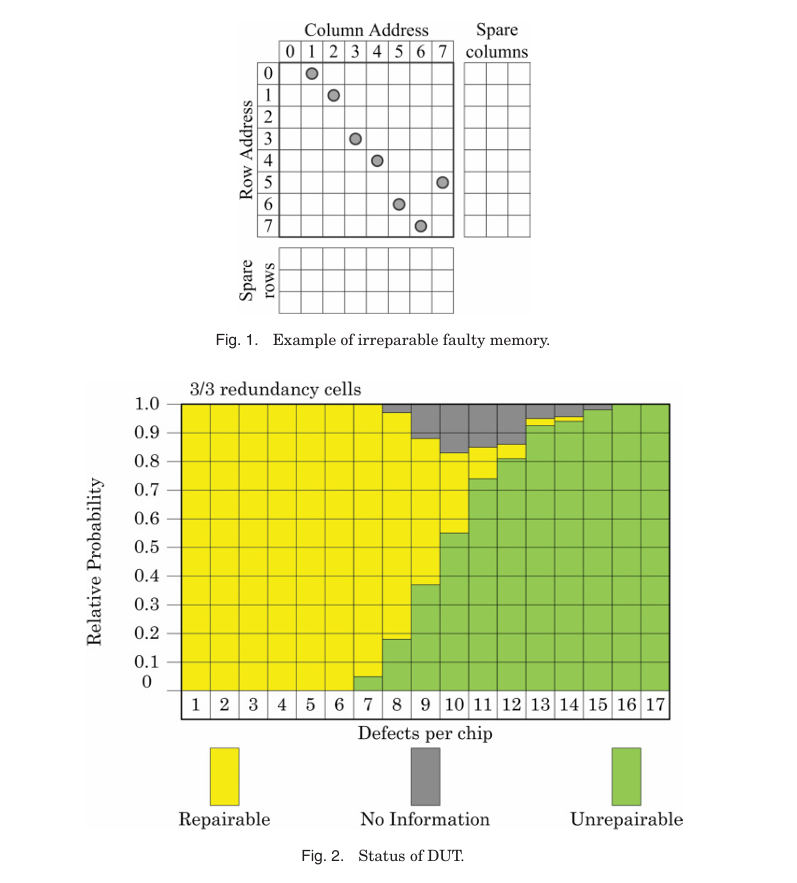
Early-abort algorithm은 irreparable 메모리를 조기에 판별해 RA(Redundancy Analysis) 과정에서 불필요한 시간 낭비를 줄이는 알고리즘이다. 일부 faulty memory는 모든 spare element를 사용해도 solution이 존재하지 않으므로 irreparable인데 사전에 reparability status를 확인하는 것이 핵심이다. 방법으로는 faulty pattern을 관찰하거나 bipartite graph의 maximum matching을 활용하며 고유 address를 가진 faulty cell 수가 total spare line(spare row + spare column)을 초과하면 수리가 불가능하다.
Figure 1에서는 3개의 spare row와 3개의 spare column이 있는 메모리에 7개의 고유 faulty cell이 있어 하나의 spare로 두 faulty cell을 동시에 수리할 수 없으므로 irreparable로 판단된다
Figure 2는 DUT(Device Under Test)에 Polya–Eggenberger 분포(A = 1.0, α = 0.6212, β = 3.230)로 생성된 faulty bit을 100,000번 테스트한 결과를 보여주며 faulty cell 수가 특정 임계값을 넘으면 irreparable 영역이 커진다.
Single-faulty-cell Filter
Single-faulty-cell filter는 single faulty cell(다른 faulty cell과 address를 공유하지 않는 결함 셀)을 분리해 RA의 분석 부담을 줄이는 알고리즘이다. Single faulty cell은 row나 column 중 하나의 spare element로 수리할 수 있는 특성이 있다.
작동 과정은 먼저 single faulty cell을 기록하고 첫 번째 단계에서 필터링해 제거한 뒤 두 번째 단계에서 나머지 faulty cell에 대한 잠재적 solution을 찾는 것이며 이후 남은 spare line(spare row와 spare column의 합)이 single faulty cell 수를 초과하는지 확인한다.
메모리에 5개의 faulty cell이 있고 그중 2개가 single faulty cell이라면 첫 단계에서 2개를 제거하고 나머지 3개를 수리한 후 남은 spare line이 2 이상이면 solution이 가능하지만, 1 이하면 irreparable이다. 이 알고리즘은 두 번째 단계의 계산량을 줄여 효율성을 높이며 single faulty cell의 단순한 수리 특성을 활용해 전체 repair solution 탐색을 간소화한다.
2.3. RA Approach의 분류
RA(Redundancy Analysis) 과정은 알고리즘에 따라 다양한 fault collection 방법으로 지원되며, RA approach는 fault collection과 RA 프로세스에 따라 세 가지 유형으로 분류된다.
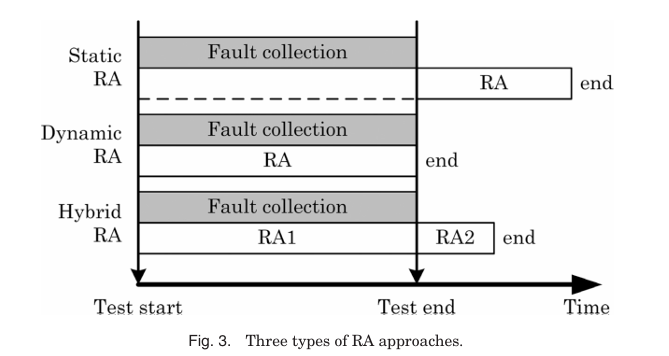
1. Static RA Approach
Static RA approach는 memory testing 동안 모든 faulty cell을 저장하기 위해 full-sized fault bitmap을 필요로 하는 방식이다. 테스트 후 fault bitmap에 저장된 모든 fault information을 RA algorithm으로 분석하며, 이 방식은 높은 repair rate를 보장하지만 큰 area overhead와 추가 search time이 요구된다. 따라서 area overhead가 중요한 BIRA(Built-In Redundancy Analysis)에는 적합하지 않다.
2. Dynamic RA Approach
Dynamic RA approach는 fault bitmap이 필요 없으며, 도착하는 모든 fault address를 즉시 spare element로 수리하는 방식이다. Memory test와 RA가 동시에 끝나며, 빠른 분석을 위해 설계되어 CRESTA [Kawagoe et al. 2000]와 ESP(Essential Spare Pivoting) [Huang et al. 2003] 같은 BIRA에서 많이 사용된다. 그러나 CRESTA는 redundancy 수에 따라 area overhead가 지수적으로 증가하고, ESP는 repair rate가 낮아지는 단점이 있다.
3. Hybrid RA Approach
Hybrid RA approach는 memory testing 중 fault address를 저장하면서 RA를 부분적으로 실행(RA1, Figure 3)하고, 남은 fault address를 RA algorithm(RA2, Figure 3)으로 분석하는 방식이다. Static RA와 dynamic RA의 장점을 결합하고 단점을 보완하며, LRM(Local Repair-Most) [Huang et al. 2003], ISF(Intelligent Solve First) [Ohler et al. 2007], SFCC(Selected Fail Count Comparison) [Jeong et al. 2009], BRANCH [Jeong et al. 2010] 같은 BIRA에서 널리 사용된다.
위에서 나온 BIRA들이 정확히 무엇인지는 나중에 확인해보자.
'DFT(Design for Testability)' 카테고리의 다른 글
| [논문리뷰] A Survey of Repair Analysis Algorithms for Memories(3) (0) | 2025.04.01 |
|---|---|
| [논문리뷰] A Survey of Repair Analysis Algorithms for Memories(2) (0) | 2025.03.30 |
| [논문 리뷰] An Overview of Processing-in-Memory Circuits for Artificial Intelligence and Machine Learning(DRAM PIM) (0) | 2025.03.24 |
| DFT(Design for Testability) (0) | 2025.03.20 |
| Memory Test(MBIST, LBIST, SCAN) (0) | 2025.03.19 |